When \(\theta=90^\circ\), \(\tan(\theta)\) is undefined. This is because at \(\theta = 90^\circ\) line L and tangent line T are parallel, so they do not intersect anywhere.
It is similar as \(\theta\) approaches -90°, with \(\tan(\theta)\) decreasing (i.e. becoming more negative) more and more rapidly.
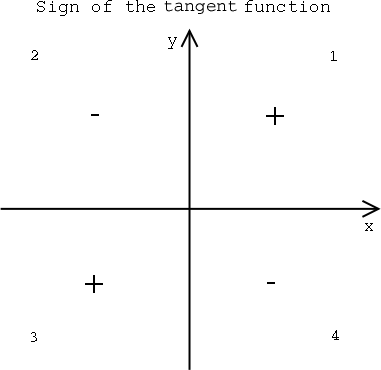The tangent function
is positive in quadrants 1 and 3 and negative in quadrants 2 and 4, as
shown. One way to help remember this is to remember that tangent is
positive when x and y are the same sign
(i.e. both positive or both negative) and negative when they
are different signs (i.e. one positive, one negative).