| previous page | back to index | next page |
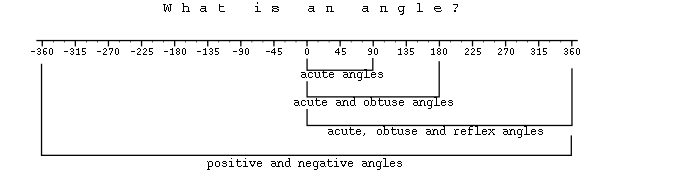
When you first learned the meaning of the word angle it was probably used to refer to the sharp corner where two lines meet. Later you learned that this was only one kind of angle, and you learned to distinguish between acute, obtuse and right angles. Later still you encountered the strange concept of a straight angle and you learned about reflex angles. Now we're also including the concept of positive and negative angles. Notice how the idea of an angle has been becoming increasingly broad.

The diagram above illustrates the range of angular measurement, in degrees, that each stage of the growing concept of an angle includes.
In fact, there is no need to stop at plus or minus 360 degrees. Why should we stop there? You might argue that an angle of, say, 365 degrees is no different from an angle of 5 degrees, and you'd be right: there is no effective difference, but they to still represent different amounts of turn. You end up facing in the same direction but 365° represents a little over a full turn while 5° is a very small turn. Similarly, the difference between an angle of 5 degrees and the corresponding reflex angle of 355 degrees (or -355 degrees, since we now care about in which direction the angle is measured): one is a small turn anti-clockwise and the other is an almost complete revolution clockwise to end up facing the same direction. In many situations we treat these as same angle just represented in a number of different ways. This is illustrated in the interactive below. The diagram on the left shows a negative angle between -180 and -540 degrees. The centre one shows an angle measuring between -180 and +180 degrees. The right diagram shows an angle measuring between +180 and +540 degrees.
Now consider this: there is no difference between the position of a point P on the unit circle for an angle \(\theta\) and the position for angle \(\theta + n \times 360^\circ\), where \(n\) is a positive or negative integer. And if point P is the same, then the projection onto the y-axis must also be the same. From this we can conclude:
\[\sin(\theta)=\sin(\theta+n\times360^\circ)\]The result of this is that \(\sin(\theta)\) is a periodic function. The function repeats itself every 360 degrees, as shown in the interactive below.
| previous page | back to index | next page |